Calcular el valor de PI con el método de Montecarlo

El método de Montecarlo es un enfoque computacional basado en el uso de números aleatorios para resolver problemas matemáticos y científicos complejos. El método se basa en la idea de simular eventos aleatorios en grandes cantidades, y de esta forma se puede obtener una solución aproximada al problema en cuestión y lo podemos ocupar para calcular el valor de PI.

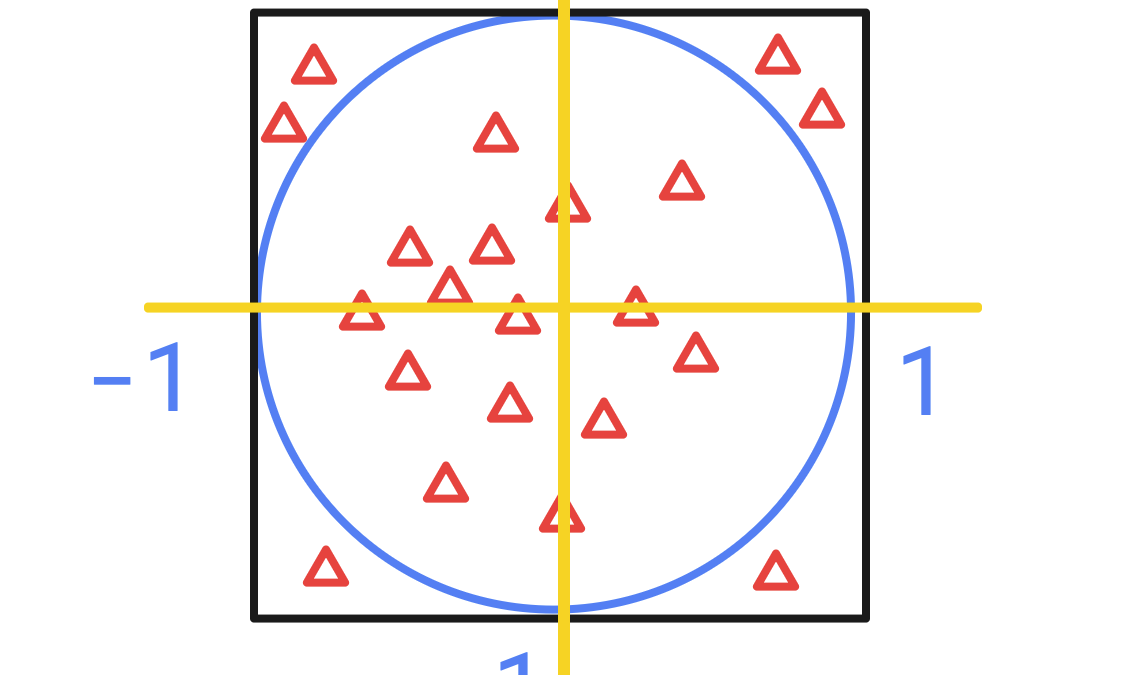
La idea es lanzar una gran cantidad de puntos aleatorios dentro de un cuadrado que circunscribe a un círculo y luego contar cuántos de esos puntos caen dentro del círculo. Utilizando la proporción entre los puntos dentro y fuera del círculo, se puede obtener una aproximación del valor de pi.

Los pasos para calcular pi utilizando el método de Montecarlo son los siguientes:

• Dibuja un cuadrado de ancho 2 y un círculo de radio 1 inscrito en el cuadrado. El centro del círculo estará en el centro del cuadrado.
• Genera un gran número de puntos aleatorios dentro del cuadrado. La forma más sencilla de hacer esto es generar coordenadas (x, y) aleatorias dentro del rango [-1, 1]. Cada punto aleatorio generado representa un lanzamiento de una aguja.

• Determina cuántos de los puntos aleatorios caen dentro del círculo. Una forma de lograr esto es si se cumple la condición de que x^2 + y^2 <= 1 
• Calcula la proporción entre los puntos dentro y fuera del círculo. Esta proporción se puede utilizar para aproximar el valor de pi. Si N es el número total de puntos lanzados y M es el número de puntos que cayeron dentro del círculo, entonces PI se puede aproximar como 4 * M / N.

La razón de esta aproximación sale de resolver la ecuación planteada de eventos favorable sobre eventos totales, y esto es equivalente al area del círculo sobre le area del cuadrado.
^N/_N = ^{PI * r ^2} / _l^2

Donde:

• l es es el largo del cuadrado, con valor 2
• r el radio del círculo con valor 1

Remplazando los valores, la ecuación queda:

^N/_N = ^PI / 4

Finalmente despejando PI queda:

PI = ^{4* M} / _N

Por ejemplo, si generamos 1 millón de puntos aleatorios dentro del cuadrado, y 785.398 de esos puntos caen dentro del círculo, entonces podemos aproximar pi como:

pi = 4 * 785.398 / 1,000,000 = 3.141592

Es importante tener en cuenta que cuanto mayor sea el número de puntos aleatorios generados, mayor será la precisión de la aproximación de pi obtenida. Por lo tanto, para obtener una buena aproximación, se recomienda utilizar un número muy grande de puntos aleatorios.

En Python podríamos escribir el código de la siguiente forma:

import random

def calc_pi(n):
    m = 0
    for i in range(n):
        x = random.uniform(-1,1)
        y = random.uniform(-1,1)
        if x*x + y*y <= 1:
            m += 1
    return 4*m / n



print(calc_pi(10000000))