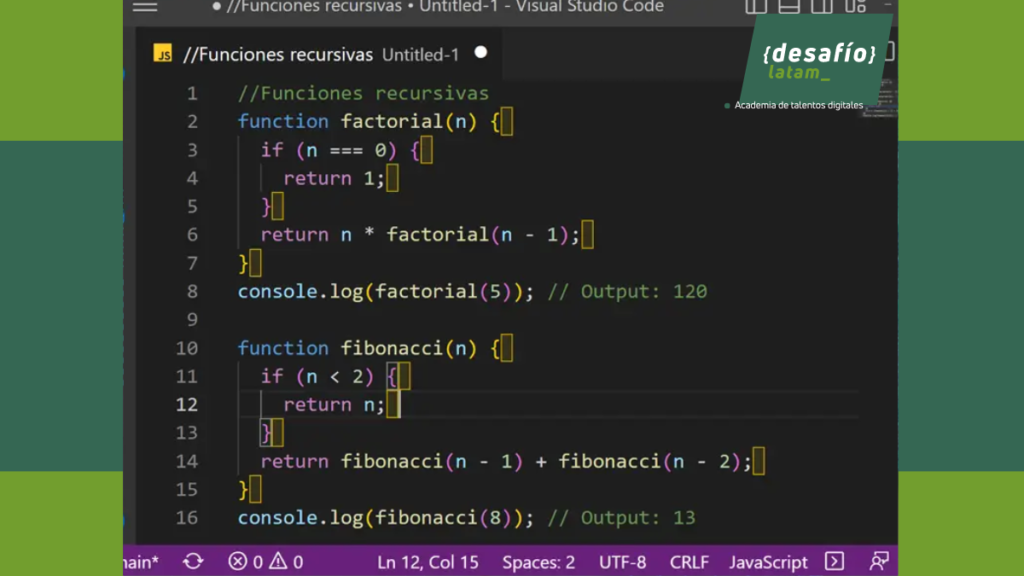
Una función recursiva se llama a sí misma durante su ejecución. Este enfoque permite a los programadores abordar problemas de manera elegante y concisa, dividiendo un problema en subproblemas más pequeños.
En muchos casos, las funciones iterativas pueden ser igualmente efectivas y más eficientes en términos de uso de recursos. La elección entre enfoques recursivos e iterativos depende del problema específico y de la claridad y eficiencia deseadas en la implementación.
Conceptos Fundamentales
Caso Base:
Cada función recursiva debe tener un caso base, una condición que detiene la recursión y proporciona un resultado directo. Sin un caso base, la recursión continuaría indefinidamente, lo que podría resultar en un desbordamiento de la pila de llamadas.
Llamadas Recursivas:
En una función recursiva, se realiza al menos una llamada a sí misma con argumentos diferentes. Cada llamada recursiva resuelve un subproblema más pequeño y contribuye al progreso hacia el caso base.
Divide y Vencerás:
El enfoque de “divide y vencerás” es fundamental en las funciones recursivas. Un problema se divide en subproblemas más pequeños, se resuelven recursivamente y luego se combinan las soluciones para obtener el resultado final.
Pila de Llamadas:
Cada llamada recursiva se agrega a la pila de llamadas. El caso base detiene la recursión y las llamadas se resuelven en orden inverso, liberando espacio en la pila. Un desbordamiento de pila puede ocurrir si la profundidad de la recursión es excesiva.
Las funciones recursivas pueden expresar soluciones de manera más clara y concisa, especialmente para problemas que pueden modelarse naturalmente de manera recursiva.
Divide y Vencerás: El enfoque divide y vencerás facilita la resolución de problemas complejos al descomponerlos en subproblemas más simples y manejables.
Reutilización de Código: La recursión permite la reutilización de código al abordar subproblemas de manera consistente.
¿Para qué sirven las funciones recursivas?
Resolución de Problemas Fractales:
Las funciones recursivas son ideales para abordar problemas que exhiben patrones repetitivos y auto-similares, como los fractales. Permiten una descripción concisa y clara de la solución al dividir el problema en partes más pequeñas.
Algoritmos de “Divide y Vencerás”:
Muchos algoritmos eficientes utilizan el enfoque de “divide y vencerás”, donde un problema se divide en subproblemas más pequeños y se resuelven de manera recursiva. Ejemplos incluyen la clasificación rápida (quicksort) y la búsqueda binaria.
Estructuras de Datos Recursivas:
Las estructuras de datos recursivas, como listas enlazadas o árboles, se definen naturalmente mediante funciones recursivas. Esto facilita la manipulación y exploración de estas estructuras.
Modelado Matemático:
Problemas matemáticos que involucran secuencias o series pueden modelarse de manera natural con funciones recursivas. Ejemplos incluyen la serie de Fibonacci, cálculos de factoriales y sucesiones matemáticas.
Recorrido de Estructuras de Datos:
Las funciones recursivas son eficientes para realizar recorridos en estructuras de datos complejas, como árboles o grafos. Esto simplifica la implementación de algoritmos de búsqueda, como la búsqueda en profundidad o la búsqueda en anchura.
Tareas Fraccionadas:
Cuando una tarea se puede dividir en subproblemas más pequeños, la recursión proporciona una forma elegante de abordar cada subproblema de manera similar. Esto mejora la legibilidad y mantenibilidad del código.
Programación Dinámica:
En el contexto de la programación dinámica, las funciones recursivas son esenciales para resolver problemas superpuestos y evitar recálculos innecesarios mediante el uso de técnicas como la memorización.
Análisis de Sistemas Fractales y Naturales:
En ciencias y análisis de sistemas complejos, las funciones recursivas pueden utilizarse para modelar fenómenos naturales y estructuras fractales.
Generación de Secuencias Infinitas:
Las funciones recursivas también pueden utilizarse para generar secuencias infinitas, como la serie de Taylor para funciones matemáticas.
Estructuras de Control de Flujo:
En algunos lenguajes de programación, la recursión se utiliza como una estructura de control de flujo alternativa, especialmente cuando se trabaja con estructuras de datos no lineales.
Para aprender más sobre el Mundo TI, conoce las carreras de Ciencia de Datos y el Análisis de Datos, que tenemos para ti, que son vitales para avanzar en el ámbito de la Inteligencia Artificial.
También te invitamos a leer sobre AI Ready y el nuevo plan de Amazon para millones de personas accedan a la Inteligencia Artificial.
Si necesitas asesorías, escríbenos al Whatsapp, ¡Tú éxito es nuestro éxito!